
Symbols | Truth tables | ICs | NOT | AND | NAND | OR | NOR | EX-OR | EX-NOR | Combinations | Substituting
Next Page: Counting Circuits
Logic gates process signals which represent true or false. Normally the positive supply voltage +Vs represents true and 0V represents false. Other terms used for the true and false states are shown in the table, it is best to be familiar with them all.
Gates are identified by their function: NOT, AND, NAND, OR, NOR, EX-OR and EX-NOR. Capital letters are normally used to make it clear that the term refers to a logic gate.
Note that logic gates are not always required because simple logic functions can be performed with switches or diodes, for example:
| Logic states | |
| True | False |
| 1 | 0 |
| High | Low |
| +Vs | 0V |
| On | Off |
The logic gate symbols used on this website are the traditional symbols with distinctive shapes making them easy to recognise. They are widely used in industry and education.
There are other sets of logic gate symbols, such as the rectangular IEC (International Electrotechnical Commission) symbols but these are rarely used despite their official status.
|
|
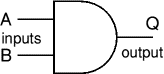
Gates have two or more inputs, except a NOT gate which has only one input. All gates have only one output. Usually the letters A, B, C and so on are used to label inputs, and Q is used to label the output. On this page the inputs are shown on the left and the output on the right.

Some gate symbols have a circle on their output which means that their function includes inverting of the output. It is equivalent to feeding the output through a NOT gate. For example the NAND (Not AND) gate symbol shown on the right is the same as an AND gate symbol but with the addition of an inverting circle on the output.
A truth table is a good way to show the function of a logic gate. It shows the output states for every possible combination of input states. The symbols 0 (false) and 1 (true) are usually used in truth tables. The example truth table shows the inputs and output of an AND gate.
There are summary truth tables below showing the output states for all types of 2-input and 3-input gates. These can be helpful if you are trying to select a suitable gate.
| Input A | Input B | Output Q |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
These summary truth tables below show the output states for all types of 2-input and 3-input gates. Note that EX-OR and EX-NOR gates can only have 2 inputs.
| Summary for all 2-input gates | |||||||
| Inputs | Output of each gate | ||||||
| A | B | AND | NAND | OR | NOR | EX-OR | EX-NOR |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| Summary for all 3-input gates | ||||||
| Inputs | Output of each gate | |||||
| A | B | C | AND | NAND | OR | NOR |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 |
Logic gates are available on ICs (chips) which usually contain several gates of the same type, for example the 4001 IC contains four 2-input NOR gates. There are several families of logic ICs and they can be split into two groups: the 4000 series and the 74 Series
To compare the different families see the ICs page.
The 4000 and 74HC families are the best for battery powered projects because they will work with a good range of supply voltages and they use very little power. However, if you are using them to design circuits and investigate logic gates please remember that all unused inputs MUST be connected to the power supply (either +Vs or 0V), this applies even if that part of the IC is not being used in the circuit!
Further details: 4000 series ICs | 74 series ICs
Rapid Electronics: 4000 series | 74 series
A NOT gate can only have one input and the output is the inverse of the input. A NOT gate is also called an inverter.
The output Q is true when the input A is NOT true: Q = NOT A
| Input A | Output Q |
| 0 | 1 |
| 1 | 0 |
|
An AND gate can have two or more inputs, its output is true if all inputs are true. The output Q is true if input A AND input B are both true: Q = A AND B
| Input A | Input B | Output Q |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
|
NAND = Not AND. This is an AND gate with the output inverted, as shown by the 'o' on the symbol output. A NAND gate can have two or more inputs, its output is true if NOT all inputs are true. The output Q is true if input A AND input B are NOT both true: Q = NOT (A AND B)
| Input A | Input B | Output Q |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
|
An OR gate can have two or more inputs, its output is true if at least one input is true. The output Q is true if input A OR input B is true (or both of them are true): Q = A OR B
| Input A | Input B | Output Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
|
NOR = Not OR. This is an OR gate with the output inverted, as shown by the 'o' on the symbol output. A NOR gate can have two or more inputs, its output is true if no inputs are true. The output Q is true if NOT inputs A OR B are true: Q = NOT (A OR B)
| Input A | Input B | Output Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
|
EXclusive-OR. This is like an OR gate but excluding both inputs being true. The output is true if inputs A and B are DIFFERENT. EX-OR gates can only have 2 inputs. The output Q is true if either input A is true OR input B is true, but not when both of them are true: Q = (A AND NOT B) OR (B AND NOT A)
| Input A | Input B | Output Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
|
EXclusive-NOR. This is an EX-OR gate with the output inverted, as shown by the 'o' on the symbol output. EX-NOR gates can only have 2 inputs. The output Q is true if inputs A and B are the SAME (both true or both false): Q = (A AND B) OR (NOT A AND NOT B)
| Input A | Input B | Output Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
|
Logic gates can be combined to produce more complex functions.
For example to produce an output Q which is true only when input A is true and input B is false, we can combine a NOT gate and an AND gate as shown.

Q = A AND NOT B
Truth tables can be used to work out the function of a combination of gates such as the system shown below:

Begin by creating a table showing all possible combinations of inputs (A, B and C in this example) with enough extra columns for each intermediate output (D and E in this example) as well as the final output (Q). Then work out all the intermediate output states, filling in the table as you do go. These intermediate outputs form the inputs to the next gate (or gates) so you can use these to work out the next output(s), in this example that is for the final output (Q).
D = NOT (A OR B)
E = B AND C
Q = D OR E = (NOT (A OR B)) OR (B AND C)
The truth table shows the intermediate outputs D and E as well as the final output Q.
| Inputs | Outputs | ||||
| A | B | C | D | E | Q |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 |
Logic gates are available on ICs which usually contain several gates of the same type, for example four 2-input NAND gates or three 3-input NAND gates. This can be wasteful if only a few gates are required unless they are all the same type. To avoid using too many ICs you can reduce the number of gate inputs or substitute one type of gate for another.

The number of inputs to a gate can be reduced by connecting two (or more) inputs together. The diagram shows a 3-input AND gate operating as a 2-input AND gate.

Reducing a NAND or NOR gate to just one input creates a NOT gate. The diagram shows this for a 2-input NAND gate.
As well as making a NOT gate, NAND or NOR gates can be combined to create any type of gate! This enables a circuit to be built from just one type of gate, either NAND or NOR. For example an AND gate is a NAND gate then a NOT gate (to undo the inverting function). Note that AND and OR gates cannot be used to create other gates because they lack the inverting (NOT) function.
To change the type of gate, such as changing OR to AND, you must do three things:
For example an OR gate can be built from NOTed inputs fed into a NAND (AND + NOT) gate.
The arrangements below show how to use NAND gates to make NOT, AND, OR and NOR gates:



This system has 3 different gates (NOR, AND and OR) so it requires three ICs, one for each type of gate.

To re-design this system using NAND gates only begin by replacing each gate with its NAND gate equivalent, as shown below:

Then simplify the system by deleting adjacent pairs of NOT gates (marked X above). This can be done because the second NOT gate cancels the action of the first:

The final system has five NAND gates and requires two ICs (with four gates on each IC). This is better than the original system which required three ICs (one for each type of gate).
Substituting NAND (or NOR) gates does not always increase the number of gates, but when it does (as in this example) the increase is usually only one or two gates. The real benefit is reducing the number of ICs required by using just one type of gate.

This book explains the inner workings of computers in an informal way, covering both hardware (the electronics) and software (languages and operating systems). It is a great introduction to what is going in inside a computer. The activities include several electronics circuits built on breadboard such as a half adder created from logic gates, a vending machine circuit and a counter built from flip-flops. As Technical Reviewer for the electronics projects I've built all of them myself and I'm very happy to recommend this book.
As an Amazon Associate, I earn from qualifying purchases. Any book you purchase through the Amazon link helps to keep this website available for everyone to use free of charge.
Next Page: Counting Circuits | Study